O
Último teorema de Fermat, ou
teorema de Fermat-Wiles, afirma que não existe nenhum conjunto de inteiros positivos
x,
y,
z e
n com
n maior que 2 que satisfaça.
-
 .
.
O
teorema deve seu nome a
Pierre de Fermat, que escreveu às margens de uma tradução de
Arithmetica de
Diofanto, ao lado do enunciado deste problema:
- "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet."
- "Encontrei uma demonstração verdadeiramente maravilhosa disto, mas esta margem é estreita demais para contê-la."
Após ter sido objeto de fervorosas pesquisas durante mais de 300 anos
(a nota acima insinuava que uma demonstração elementar era possível — o
que atiçou a curiosidade de todos), ele foi finalmente demonstrado em
1994 pelo matemático
britânico Andrew Wiles.
A grande maioria dos matemáticos acredita hoje que Fermat estava
enganado: a prova utiliza ferramentas matemáticas bastante elaboradas da
Teoria dos números — abrangendo
curvas elípticas,
formas modulares e
representações galoisianas (termo derivado de
Évariste Galois, matemático francês) — as quais ainda não existiam na época em que viveu Fermat.
Mais precisamente, Wiles provou um caso particular (para curvas ditas semi-estáveis) da
Conjectura de Shimura-Taniyama-Weil, pois sabia-se já havia algum tempo que este caso implicava o teorema.
Ainda não é conhecida nenhuma aplicação deste teorema. Ele toma um
valor importante, no entanto, devido às ideias e às ferramentas
matemáticas que foram inventadas e desenvolvidas para prová-lo. Pode-se
entender este teorema graficamente considerando-se a curva da equação

quando
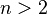
, essa curva não passa por nenhum ponto com coordenadas racionais diferentes de zero.

![\sqrt[b]{x^a}](http://upload.wikimedia.org/math/1/a/7/1a7bc7f37eb17dc98d89471aa17dd459.png) =
= 
![x^{1,5} = x^{\frac{15}{10}} = \sqrt[10]{x^{15}}](http://upload.wikimedia.org/math/c/3/9/c3913eaa56c7855e591283cd0f00eae9.png)

 .
. quando
quando 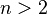 , essa curva não passa por nenhum ponto com coordenadas racionais diferentes de zero.
, essa curva não passa por nenhum ponto com coordenadas racionais diferentes de zero.






