P.A ou P.G ?
Determine o próximo número da sequência:
2,10,12,16,17,18,19,...
Determine o próximo número da sequência:
5,11,19,29,41,...
E ai qual o próximo numero???
Resposta aqui

 e
e  .
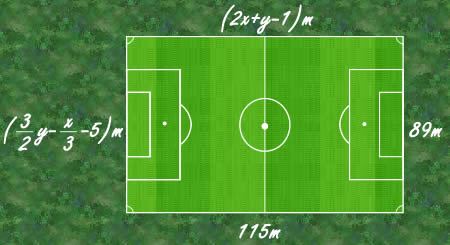
.




 .
. definida por
definida por  .
. de tais que
de tais que  .
.








 e
e  são dois objetos que têm a mesma imagem.
são dois objetos que têm a mesma imagem.


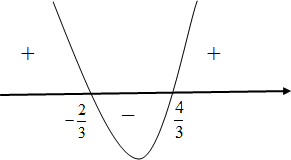
![S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[ S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[](http://www.atividadesdematematica.com/images/joomlatex/0f5d3a88f188b78ada22d18983083410.gif)

Copyright ©
Matemática para aprender | Powered by Blogger
Design by SimpleWpThemes | Blogger Theme by NewBloggerThemes.com