0

Exercício bem Legal de Função

By Smatias / Posted on 22:10 / ,

Função Quadrática

Exercício 1
Considere a função h definida por h\left( x \right) = 2{x^2} - \frac{4}{3}x.
Determine:
1. os zeros da função.
2. o vértice e o eixo de simetria da parábola que representa graficamente a função.
3. dois objetos, distintos dos zeros, que tenham a mesma imagem.
4. os valores x de tais que h\left( x \right) > \frac{{16}}{9} .

Resolução do exercício de matemática:

1.

h\left( x \right) = 0 \Leftrightarrow 2{x^2} - \frac{4}{3}x = 0 \Leftrightarrow x\left( {2x - \frac{4}{3}} \right) = 0 \Leftrightarrow x = 0 \vee 2x - \frac{4}{3} = 0 \Leftrightarrow

\Leftrightarrow x = 0 \vee 2x = \frac{4}{3} \Leftrightarrow x = 0 \vee x = \frac{2}{3}

S = \left\{ {0,\frac{2}{3}} \right\}

2.

h\left( x \right) = 2{x^2} - \frac{4}{3}x = 2\left( {{x^2} - \frac{2}{3}x} \right) = 2\left( {{x^2} - \frac{2}{3}x + {{\left( {\frac{1}{3}} \right)}^2} - {{\left( {\frac{1}{3}} \right)}^2}} \right) =

= 2\left( {{x^2} - \frac{2}{3}x + {{\left( {\frac{1}{3}} \right)}^2}} \right) - {\left( {\frac{1}{3}} \right)^2} \times 2 = 2{\left( {x - \frac{1}{3}} \right)^2} - \frac{2}{9}

Coordenadas do vértice:   V\left( {\frac{1}{3}, - \frac{2}{9}} \right)

Eixo de simetria:   x = \frac{1}{3}

3.

Os objetos pretendidos têm que estar à mesma distância do eixo de simetria.
Por exemplo:

\frac{1}{3} - 2 = - \frac{5}{3}

\frac{1}{3} + 2 = \frac{7}{3}

Logo, - \frac{5}{3} e \frac{7}{3}  são dois objetos que têm a mesma imagem.

4.

h\left( x \right) > \frac{{16}}{9} \Leftrightarrow 2{x^2} - \frac{4}{3}x > \frac{{16}}{9} \Leftrightarrow 2{x^2} - \frac{4}{3}x - \frac{{16}}{9} > 0

Cálculo auxiliar:

2{x^2} - \frac{4}{3}x - \frac{{16}}{9} = 0 \Leftrightarrow x = \frac{{\frac{4}{3} \pm \sqrt {{{\left( { - \frac{4}{3}} \right)}^2} - 4 \times 2 \times \left( { - \frac{{16}}{9}} \right)} }}{{2 \times 2}} \Leftrightarrow

\Leftrightarrow x = \frac{{\frac{4}{3} \pm 4}}{4} \Leftrightarrow x = \frac{{\frac{{16}}{3}}}{4} \vee x = \frac{{ - \frac{8}{3}}}{4} \Leftrightarrow x = \frac{4}{3} \vee x = - \frac{2}{3}

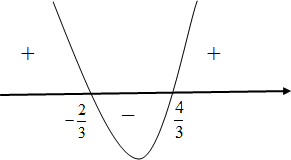
Funções

S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[

0 Comments:

Postar um comentário

Assinar: Postar comentários (Atom)