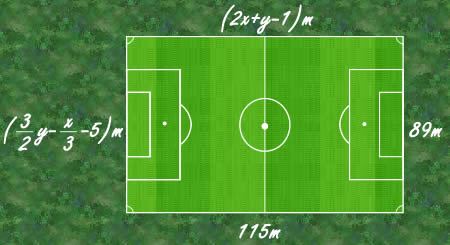
Na Figura está representado o retângulo de jogo de um campo de futebol. Determine  e
e  .
.
Resolução do exercício de matemática




Portanto, .
.
 e
e  .
.
Resolução do exercício de matemática




Portanto,
 .
. e
e  .
.




 .
. definida por
definida por  .
. de tais que
de tais que  .
.








 e
e  são dois objetos que têm a mesma imagem.
são dois objetos que têm a mesma imagem.


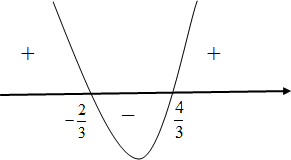
![S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[ S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[](http://www.atividadesdematematica.com/images/joomlatex/0f5d3a88f188b78ada22d18983083410.gif)


Copyright ©
Matemática para aprender | Powered by Blogger
Design by SimpleWpThemes | Blogger Theme by NewBloggerThemes.com