Estudo da Função seno
Considera a função real de variável real , definida por
, definida por  .
.
1. Indica o dominio de  .
.
 .
.2. Esboça o gráfico de
 .
.3. A partir do gráfico obtido, faz um estudo da função
 quanto a:
quanto a:
a. Período
b. Zeros
c. Extremos e extremantes
d. Paridade
e. Injetividade
f. Contradomínio
Resolução do Exercício de Matemática1. Sendo o domínio de uma função o conjunto dos valores que podemos atribuir à variável independente
 , temos que
, temos que  .
.2. Para representar graficamente a função podemos utilizar o estudo efetuado no círculo trignométrico, relativo aos extremos e zeros.
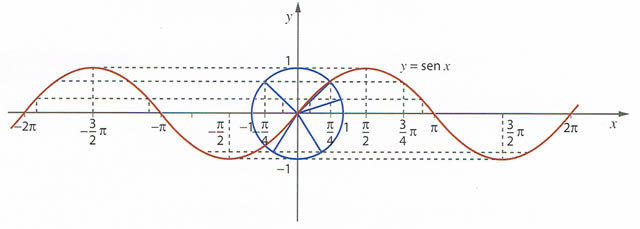
3. Com base na representação gráfica apresentada podemos afirmar que:
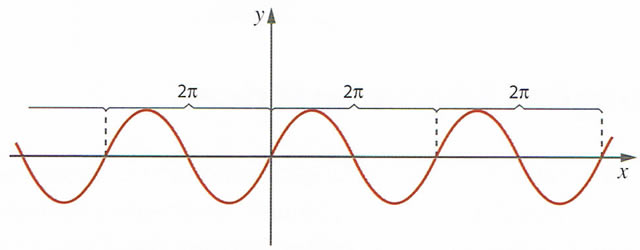
a. Periodicidade:  é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo  , o que significa que a função seno assume os mesmos valores de
, o que significa que a função seno assume os mesmos valores de  em
em  , isto é
, isto é 
 é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo  , o que significa que a função seno assume os mesmos valores de
, o que significa que a função seno assume os mesmos valores de  em
em  , isto é
, isto é 
b. Zeros:  admite zeros em
admite zeros em 
 admite zeros em
admite zeros em 
c. Extremos: Os extremos e extremantes de  são:
são:
 são:
são:
i. Mínimo = -1.
ii. Minimizantes: 

iii. Máximo = 1.
iv. Maximizantes: 

d. Paridade:  é uma função ímpar, pois
é uma função ímpar, pois  . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
 é uma função ímpar, pois
é uma função ímpar, pois  . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
e. Injetividade:  não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 
 não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 
f. Contradomínio: 
![= \left[ { - 1,1} \right] = \left[ { - 1,1} \right]](http://www.atividadesdematematica.com/images/joomlatex/c421c8837a12e0801c59c41a50ee6545.gif)

![= \left[ { - 1,1} \right] = \left[ { - 1,1} \right]](http://www.atividadesdematematica.com/images/joomlatex/c421c8837a12e0801c59c41a50ee6545.gif)

 .
.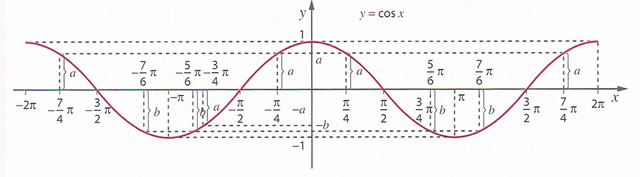

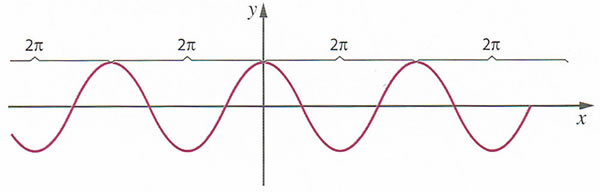



 . Graficamente esta propriedade traduz-se pela existência de simetria relativamente ao eixo das ordenadas.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente ao eixo das ordenadas.






