Número de Ouro
 A história deste número irracional e enigmático se
entrelaça e ao mesmo tempo se perde dentro da antiguidade, por causa da
necessidade e da procura de uma perfeição, uma beleza, um equilíbrio e uma harmonia
que é perceptível na natureza das coisas. Por muitos anos as pessoas procuravam
padrões para as criações mas, não se achava tal padrão, embora ele sempre
estivesse lá desde os tempos mais remotos da natureza. Sua procura sempre foi
uma meta, tendo em vista que, sua descoberta tenha sido um mistério porque não
se sabe ao certo quando e quem descobriu esta relação natural e nem que deu
origem ao número áureo. A insistente procura e investigação da razão que
justificasse o número de ouro como modelo e padrão de beleza, fez com que o
matemático alemão Zeizing formulasse o seguinte principio:
A história deste número irracional e enigmático se
entrelaça e ao mesmo tempo se perde dentro da antiguidade, por causa da
necessidade e da procura de uma perfeição, uma beleza, um equilíbrio e uma harmonia
que é perceptível na natureza das coisas. Por muitos anos as pessoas procuravam
padrões para as criações mas, não se achava tal padrão, embora ele sempre
estivesse lá desde os tempos mais remotos da natureza. Sua procura sempre foi
uma meta, tendo em vista que, sua descoberta tenha sido um mistério porque não
se sabe ao certo quando e quem descobriu esta relação natural e nem que deu
origem ao número áureo. A insistente procura e investigação da razão que
justificasse o número de ouro como modelo e padrão de beleza, fez com que o
matemático alemão Zeizing formulasse o seguinte principio:
"Para que um
todo dividido em duas partes desiguais pareça belo do ponto de vista da forma,
deve apresentar à parte menor e a maior a mesma relação que entre esta e o
todo."
Zeizing – (1855)
Suas origens são
antiguíssimas no Egito, por exemplo nas pirâmides de Gizé, a razão entre a
altura de uma face e metade do lado da base da grande pirâmide é igual ao
número de ouro, ou seja, foram construídas levando-se em conta a Divina
proporção.
O interessante é que no papiro encontravam-se
citações de uma razão sagrada como é o caso de Rhind, um documento Egípcio que
está em papiro e encontra–se no museu britânico e neste documento egípcio de
cerca de 1650
a.C
temos 85 problemas matemáticos copiados de um trabalho mais antigo por um
escriba Ahmes. O documento refere-se a uma razão sagrada que se crê ser o
número de ouro. No próprio Egito na tumba de Khesi-Ra, um sacerdote egípcio do deus GOR, o deus da harmonia, que
viveu por volta de 2700 a.c. foi encontrado um cânone arquitetônico que prova conhecimento
da proporção áurea e provavelmente do teorema de Pitágoras. Passando
pelo mundo para mais longe, desde a Grécia antiga os homens já faziam uso da
proporção. Os gregos consideraram que o retângulo cujos lados expressavam esta
relação, apresentava uma especial harmonia e um equilíbrio da estética. O
retângulo que apresentava esta harmonia em sua estrutura foi nomeado de
retângulo áureo ou retângulo de ouro, considerando esta harmonia como uma
virtude excepcional. Centenas de anos atrás entre 447 e 433 A.C. o Parthenon
Grego foi construído usando este numero. Na fachada do Parthenon, contem o
retângulo de ouro na razão entre largura e altura, isso revela que desde
aqueles tempos já se procurava a construção de algo harmonioso. O arquiteto
deste templo foi Fídias, o grego que teve a primeira letra do seu nome, a letra
grega (Phi maiúsculo), para ser designada como
nomenclatura da razão áurea e quem teve esta idéia foi Mark Barr, no começo do século XX, por que no
princípio para essa razão era a letra grega (tau) que significa o corte.
Phi foi um dos primeiros números irracionais
que se teve consciência. Os pitagoricos também o usaram na construção da
estrela pentagonal. Na construção da sua estrela pentagonal os pitagoricos não
conseguiram exprimir o quociente entre dois números inteiros, a razão existente
entre o lado do pentágono regular estrelado e o lado do pentágono regular
inscritos numa circunferência. Quando chegaram a esta conclusão ficaram muito
espantados, pois tudo isto era muito contrário a toda lógica que conheciam e
defendiam, pois acreditavam que o mundo fosse construído por números inteiros.
Pitágoras de Samos adotou um pentagrama como símbolo de sua escola, que é a
estrela de cinco pontas formada por um pentágono regular.
No pentágono regular as diagonais se
seccionam mutuamente na proporção áurea, são os seus cinco menores triângulos e
a razão entre o lado do pentágono que circunscreve o pentagrama e o lado do
pentágono interno, formado pelas diagonais, é igual a φ². A escola pitagórica escolheu o duodecaedro como sólido
perfeito pois este se baseia na Relação áurea. O duodecaedro possui 12 faces e
60 vértices, sendo construído sobre um pentágono regular.
Na Itália
Leonardo Da Vinci (1452-1519) utilizava esta proporção em suas obras,
trazendo a excelência em suas criações usando a proporção áurea como
ferramenta. Observando cautelosamente as
mais famosas e impressionantes obras como a Mona Lisa, o Homem Virtruviano e A Ultima Ceia, tem a
divina proporção com o retângulo áurea se observadas minuciosamente.
Um vídeo muito legal do assunto AQUIIII
Um vídeo muito legal do assunto AQUIIII


 , definida por
, definida por  .
. , temos que
, temos que  .
.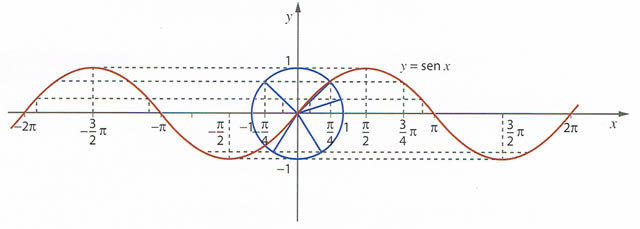
 , o que significa que a função seno assume os mesmos valores de
, o que significa que a função seno assume os mesmos valores de 
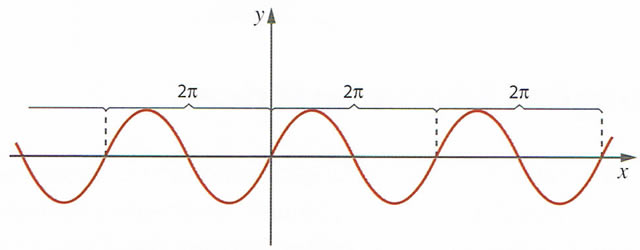



 . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.

![= \left[ { - 1,1} \right] = \left[ { - 1,1} \right]](http://www.atividadesdematematica.com/images/joomlatex/c421c8837a12e0801c59c41a50ee6545.gif)









