Software educacional estão se tornando mais comum entre professores e alunos. Ajudar o aluno a resolver as coisas aprendidas em sala de aula .
Valeu!!!
Baixe também para auxiliar em seus estudos.
Geogebra
Poly 1.12
Graph
Math Mechanixs
 A história deste número irracional e enigmático se
entrelaça e ao mesmo tempo se perde dentro da antiguidade, por causa da
necessidade e da procura de uma perfeição, uma beleza, um equilíbrio e uma harmonia
que é perceptível na natureza das coisas. Por muitos anos as pessoas procuravam
padrões para as criações mas, não se achava tal padrão, embora ele sempre
estivesse lá desde os tempos mais remotos da natureza. Sua procura sempre foi
uma meta, tendo em vista que, sua descoberta tenha sido um mistério porque não
se sabe ao certo quando e quem descobriu esta relação natural e nem que deu
origem ao número áureo. A insistente procura e investigação da razão que
justificasse o número de ouro como modelo e padrão de beleza, fez com que o
matemático alemão Zeizing formulasse o seguinte principio:
A história deste número irracional e enigmático se
entrelaça e ao mesmo tempo se perde dentro da antiguidade, por causa da
necessidade e da procura de uma perfeição, uma beleza, um equilíbrio e uma harmonia
que é perceptível na natureza das coisas. Por muitos anos as pessoas procuravam
padrões para as criações mas, não se achava tal padrão, embora ele sempre
estivesse lá desde os tempos mais remotos da natureza. Sua procura sempre foi
uma meta, tendo em vista que, sua descoberta tenha sido um mistério porque não
se sabe ao certo quando e quem descobriu esta relação natural e nem que deu
origem ao número áureo. A insistente procura e investigação da razão que
justificasse o número de ouro como modelo e padrão de beleza, fez com que o
matemático alemão Zeizing formulasse o seguinte principio:  , definida por
, definida por  .
. .
. .
. quanto a:
quanto a: , temos que
, temos que  .
.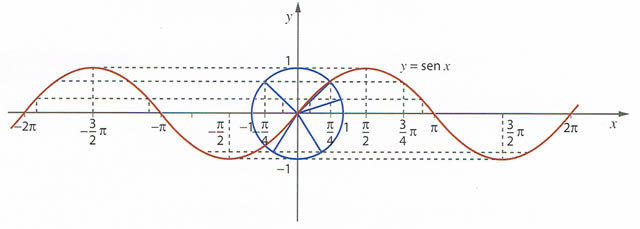
 é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo  , o que significa que a função seno assume os mesmos valores de
, o que significa que a função seno assume os mesmos valores de  em
em  , isto é
, isto é 
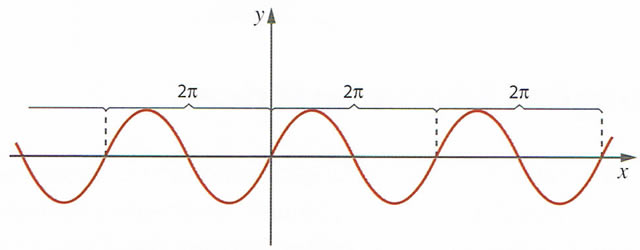
 admite zeros em
admite zeros em 
 são:
são:

 é uma função ímpar, pois
é uma função ímpar, pois  . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial. não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 

![= \left[ { - 1,1} \right] = \left[ { - 1,1} \right]](http://www.atividadesdematematica.com/images/joomlatex/c421c8837a12e0801c59c41a50ee6545.gif)

Copyright ©
Matemática para aprender | Powered by Blogger
Design by SimpleWpThemes | Blogger Theme by NewBloggerThemes.com