O Último teorema de Fermat, ou teorema de Fermat-Wiles, afirma que não existe nenhum conjunto de inteiros positivos x, y, z e n com n maior que 2 que satisfaça.
-
 .
.
- "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet."
- "Encontrei uma demonstração verdadeiramente maravilhosa disto, mas esta margem é estreita demais para contê-la."
Mais precisamente, Wiles provou um caso particular (para curvas ditas semi-estáveis) da Conjectura de Shimura-Taniyama-Weil, pois sabia-se já havia algum tempo que este caso implicava o teorema.
Ainda não é conhecida nenhuma aplicação deste teorema. Ele toma um valor importante, no entanto, devido às ideias e às ferramentas matemáticas que foram inventadas e desenvolvidas para prová-lo. Pode-se entender este teorema graficamente considerando-se a curva da equação
 quando
quando 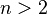 , essa curva não passa por nenhum ponto com coordenadas racionais diferentes de zero.
, essa curva não passa por nenhum ponto com coordenadas racionais diferentes de zero.














