0

Hipótese de Riemann

By Smatias / Posted on 12:19 /

Hipótese de Riemann

Provar que uma fórmula está incorreta é até fácil. O desafio, aqui, é provar que ela está totalmente correta. O alemão Georg Bernhard Riemmann acreditou ter finalmente descoberto a fórmula matemática para se descobrir os números primos - aqueles que só podem ser divididos por um ou por eles mesmos. Essa sequência sempre desafiou os matemáticos, porque não parece haver lógica nessa sequência. Ou não parecia, até Riemmann propor sua hipótese.

A questão é que não se encontrou um meio de provar sua correção senão submetendo cada número ao teste. Isso já foi feito com os primeiros 1,5 bilhão de números e continua correta, mas ainda é pouco para se provar que ela é totalmente verdadeira. Quem conseguir provar que a hipótese é mesmo verdadeira ou está totalmente errada - lembre-se, basta que um dos números não encaixe - vence o desafio da hipótese de Riemmann.
Read More
0

Segredos da Função Cosseno

By Smatias / Posted on 14:58 /

Estudo da Função cosseno

Considera a função real de variável real f, definida por f(x) = cos{\text{ }}x.
1. Indica o dominio de f.

2. Esboça o gráfico de f.

3. A partir do gráfico obtido, faz um estudo da função f quanto a:
a. Período
b. Zeros
c. Extremos e extremantes
d. Paridade
e. Injetividade
f. Contradomínio
Resolução do Exercício de Matemática
1. Sendo o domínio de uma função o conjunto dos valores que podemos atribuir à variável independente x, temos que {D_f} = \mathbb{R}.
2. Para representar graficamente a função podemos utilizar o estudo efetuado no círculo trignométrico, relativo aos extremos e zeros.
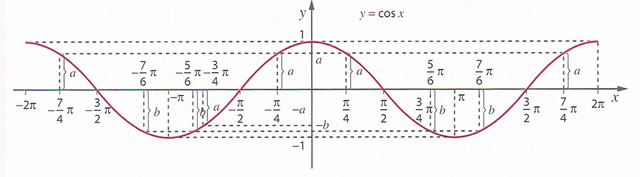
estudo-da-funcao-cosseno-x
3. Com base na representação gráfica apresentada podemos afirmar que:
a. Periodicidade: fé uma função periódica de período positivo mínimo 2\pi , o que significa que a função cosseno assume os mesmos valores de 2\pi  em 2\pi , isto é cos(x) = cos(x + k \times 2\pi ),k \in \mathbb{Z}
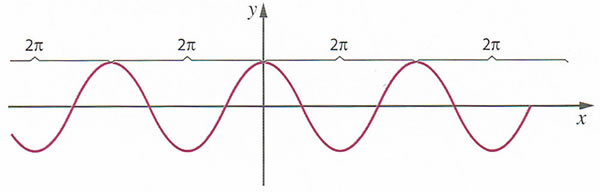
periodicidade-funcao-cosseno-x
b. Zeros: fadmite zeros em x =\frac{\pi}{2} + k\pi \text{, } k\in \mathbb{Z}
c. Extremos: Os extremos e extremantes de fsão:
i. Mínimo = -1.
ii. Minimizantes: x = \pi + k \times 2\pi ,k \in \mathbb{Z}
iii. Máximo = 1.
iv. Maximizantes: x = k \times 2\pi ,k \in \mathbb{Z}
d. Paridade: fé uma função par, pois cos( - x) = cos{\text{ }}x,\forall x \in \mathbb{R}. Graficamente esta propriedade traduz-se pela existência de simetria relativamente ao eixo das ordenadas.
e. Injetividade: fnão é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo cos( - \frac{\pi}{2} ) = cos(\frac{\pi}{2}) = 0
f. Contradomínio:D_f^' = \left[ { - 1,1} \right]
Read More
0

2 Pequenos Problemas para melhorar o raciocínio

By Smatias / Posted on 13:36 /

Problemas para resolver

 1) Um pequeno caminhão pode carregar 50 sacos de areia ou 400 tijolos. Se foram colocados no caminhão 32 sacos de areia, quantos tijolos pode ainda ele carregar?




2) Dois pais e dois filhos foram pescar. Cada um pescou um peixe, sendo que ao todo foram pescados 3 peixes. Como isso é possível?

   
1 Resposta:

1 saco de areia = 8 tijolos.


Se o caminhão pode carregar ainda 18 sacos então pode carregar 18 ´ 8 = 144 tijolos.

2 Resposta:

Três pessoas estavam pescando: filho, pai e avô.

O pai é filho e pai ao mesmo tempo. Há dois filhos (filho e pai) e dois pais (pai e avô).
Nosso app Matcalculo.APP

 Qual a sua dúvida?
Função AFIM ou QUADRÁTICA, MEDIDAS DE COMPRIMENTO
 MEDIDAS DE ÁREA, MEDIDAS VOLUME, MEDIDAS DE CAPACIDADE LITROS
POTENCIAÇÃO, LOG, P.A, PRODUTO NOTÁVEL, CURIOSIDADE Qual a sua dúvida?

NUMERO 13, PARADOXO DO ANIVERSÁRIO, COMO GANHAR MAIS DE R$ 3.OOO POR MÊS
MAS SE VOCÊ QUER ESTUDAR E REALIZAR SEUS SONHOS COM UMA RENDA EXTRA, ENTÃO NÃO PERCA TEMPO CONHEÇA A UP! ESSÊNCIA

Read More
Assinar: Postagens (Atom)