Nosso canal do YouTube!!
0
Um Curso De Cálculo - Vol 1, 2, 3 e 4 - Hamilton L. Guidorizzo
0
CONFIRA O CANAL MATCÁLCULO
Matemática Moderna Vol 1 http://encurta.net/fC01s54w
Matemática Moderna Vol 2 http://encurta.net/TbjVCJ
Matemática moderna Vol 3 http://encurta.net/lUgHS
Matemática - Manoel Paiva
Manoel Paiva
CONFIRA O CANAL MATCÁLCULO
Matemática Moderna Vol 1 http://encurta.net/fC01s54w
Matemática Moderna Vol 2 http://encurta.net/TbjVCJ
Matemática moderna Vol 3 http://encurta.net/lUgHS
0
Matemática Contextos e Aplicações Dante
Matemática Contextos e Aplicações Dante
http://encurta.net/cdjOMm
0
Basta clicar
Apostilas
By Smatias / Posted on 19:23 / Apostilas
As melhores apostilas de vestibular.
Basta clicar
0
P.A ou P.G ?
Determine o próximo número da sequência:
2,10,12,16,17,18,19,...
Determine o próximo número da sequência:
5,11,19,29,41,...
E ai qual o próximo numero???
Resposta aqui
Determine...
By Smatias / Posted on 01:19 / Exercício
P.A ou P.G ?
Determine o próximo número da sequência:
2,10,12,16,17,18,19,...
Determine o próximo número da sequência:
5,11,19,29,41,...
E ai qual o próximo numero???
Resposta aqui
0
Um bolsa tem 27 bolas de bilhar que parecem idênticas. É certo que há uma bola defeituosa que pesa mais que as outras. Dispomos de uma balança com 2 pratos. Demonstre que se pode localizar a bola defeituosa como somente três pesagens.
Resposta aqui!!!1
Um bolsa tem 27 bolas de bilhar que parecem idênticas. É certo que há uma bola defeituosa que pesa mais que as outras ...Bolas com defeito...
By Smatias / Posted on 18:05 / Exercício
Um bolsa tem 27 bolas de bilhar que parecem idênticas. É certo que há uma bola defeituosa que pesa mais que as outras. Dispomos de uma balança com 2 pratos. Demonstre que se pode localizar a bola defeituosa como somente três pesagens.
Resposta aqui!!!1
0
Buscando água, uma rã caiu em um poço de 30 metros de profundidade. Na sua busca por sobrevivência, a obstinada rã conseguia subir 3 metros cada dia, sendo que a noite resbalava e descia 2 metros. Quantos dias a rã demorou para sair do poço?
Resposta
Rã em apuros, exercício básico
By Smatias / Posted on 22:11 / Exercício
Olha isso
Buscando água, uma rã caiu em um poço de 30 metros de profundidade. Na sua busca por sobrevivência, a obstinada rã conseguia subir 3 metros cada dia, sendo que a noite resbalava e descia 2 metros. Quantos dias a rã demorou para sair do poço?
Resposta
0
Você já pensou sobre o infinito? Imagine um hotel com infinitos quartos, o quarto número 1, o quarto número 2, o número 3 e assim por diante. Imagine agora que este hotel está lotado. Chega então um novo casal de hóspedes, como alojá-los? Se fosse um hotel comum, um hotel finito não haveria jeito. No hotel infinito basta pedir a cada hóspede o favor de se mudar para o quarto ao lado: os hóspedes do quarto 1 passam para o quarto 2, os do 2 passam para o quarto 3 e assim por diante. O quarto 1 fica vago para receber casal recém chegado. Incrível, não? Esta questão, conhecida como Paradoxo do Hotel de Hilbert, foi bolada pelo alemão David Hilbert que viveu entre 1862 e 1943 e foi um dos grandes matemáticos de todos os tempos. Agora responda você: e se chegasse no Hotel de Hilbert já lotado o ônibus infinito de uma excursão Hilbertiana, trazendo infinitos novos hóspedes? Será que você conseguiria acomodá-los todos sem desalojar os que já estão no hotel?
CONFIRA O CANAL MATCÁLCULO

Resposta
Você já pensou sobre o infinito? Imagine um hotel com infinitos quartos, o quarto número
By Smatias / Posted on 16:00 / Curiosidade, Exercício
Hotel de Hilbert é infinito...
Você já pensou sobre o infinito? Imagine um hotel com infinitos quartos, o quarto número 1, o quarto número 2, o número 3 e assim por diante. Imagine agora que este hotel está lotado. Chega então um novo casal de hóspedes, como alojá-los? Se fosse um hotel comum, um hotel finito não haveria jeito. No hotel infinito basta pedir a cada hóspede o favor de se mudar para o quarto ao lado: os hóspedes do quarto 1 passam para o quarto 2, os do 2 passam para o quarto 3 e assim por diante. O quarto 1 fica vago para receber casal recém chegado. Incrível, não? Esta questão, conhecida como Paradoxo do Hotel de Hilbert, foi bolada pelo alemão David Hilbert que viveu entre 1862 e 1943 e foi um dos grandes matemáticos de todos os tempos. Agora responda você: e se chegasse no Hotel de Hilbert já lotado o ônibus infinito de uma excursão Hilbertiana, trazendo infinitos novos hóspedes? Será que você conseguiria acomodá-los todos sem desalojar os que já estão no hotel?
CONFIRA O CANAL MATCÁLCULO

Resposta
0
Deseja-se descobrir quantos degraus são visíveis numa escada rolante. Para isso foi feito o seguinte
By Smatias / Posted on 11:42 / Exercício
Deseja-se descobrir quantos degraus são visíveis numa escada rolante. Para isso foi feito o seguinte:
Deseja-se descobrir quantos degraus são
visíveis numa escada rolante. Para isso foi feito o seguinte: duas pessoas
começaram a subir a escada juntas, uma subindo um degrau de cada vez enquanto
que a outra subia dois . Ao chegar ao topo, o primeiro contou 21 degraus
enquanto o outro 28. Com esses dados foi possível responder a questão. Quantos
degraus são visíveis nessa escada rolante? (obs: a escada está andando).
0
Questão de concurso
By Smatias / Posted on 12:40 / Exercício
CONCURSO SECRETARIA MUNICIPAL DE SAÚDE/2005 – CESGRANRIO) – (questão de sistemas de medidas)
Raquel saiu de casa às 13h 45min, caminhando até o curso de inglês que fica a 15 minutos de sua casa, e chegou na hora da aula cuja duração é de uma hora e meia. A que horas terminará a aula de inglês?
a) 14h
b) 14h 30min
c) 15h 15min
d) 15h 30min
e) 15h 45min
Solução:
Basta somarmos todos os valores mencionados no enunciado do teste, ou seja:
13h 45min + 15 min + 1h 30 min = 15h 30min
Gabarito: D
Raquel saiu de casa às 13h 45min, caminhando até o curso de inglês que fica a 15 minutos de sua casa, e chegou na hora da aula cuja duração é de uma hora e meia. A que horas terminará a aula de inglês?
a) 14h
b) 14h 30min
c) 15h 15min
d) 15h 30min
e) 15h 45min
Solução:
Basta somarmos todos os valores mencionados no enunciado do teste, ou seja:
13h 45min + 15 min + 1h 30 min = 15h 30min
Gabarito: D
0
Com os algarismos x, y e z formam-se os números de dois algarismos xy e yx, cuja soma é o número de três algarismos zxz. Quanto valem x, y e z?
Esta é bem inteligente..
CONFIRA O CANAL MATCÁLCULO
Resposta AQUI
Com os algarismos x, y e z formam-se os números de dois algarismos xy e yx, cuja soma é
By Smatias / Posted on 22:56 / Exercício
Desafio do X,Y,Z
Com os algarismos x, y e z formam-se os números de dois algarismos xy e yx, cuja soma é o número de três algarismos zxz. Quanto valem x, y e z?
Esta é bem inteligente..
CONFIRA O CANAL MATCÁLCULO
Resposta AQUI
0
(A) 14 (B) 13 (C) 10 (D) 8 anos e 4 meses (E) 7 anos e 6 meses
essa deu um pouco de trabalho...
É interresante tentar antes de ver a resposta...
Mas a resposta é jachkero-agua-sua-idade-e.html
Problema com Idades
By Smatias / Posted on 02:10 / Exercício
Problema com Idade sempre é legal
A idade atual de Jachkero àgua é a diferença entre 5/8 da idade que ele terá daqui a 18 anos e os 2/3 da idade que ele teve há 5 anos. A idade de Jachkero àgua é:(A) 14 (B) 13 (C) 10 (D) 8 anos e 4 meses (E) 7 anos e 6 meses
essa deu um pouco de trabalho...
É interresante tentar antes de ver a resposta...
Mas a resposta é jachkero-agua-sua-idade-e.html
1
Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?
Resposta
Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se
By Smatias / Posted on 18:13 / Exercício
E agora
Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se, repartindo antes o vinho igualmente.Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?
Resposta
0
A soma de todas as raízes da equação
By Smatias / Posted on 00:33 / Exercício
A soma de todas as raízes da equação x^4 - 25x^2 + 144 = é igual a
a) 16 b) 0 c) 9 d) 49 e) 25
CONFIRA O CANAL MATCÁLCULO
Solução:
Em um polinômio da forma: A.x^n + B.x^n-1 + C.x^n-2 + ..., a soma de suas raízes é dada pelo quociente -
B/A. No polinômio em questão, o coeficiente do termo x3 é nulo, logo, a soma de todas as suas raízes
é zero.
Resposta: letra b.
a) 16 b) 0 c) 9 d) 49 e) 25
CONFIRA O CANAL MATCÁLCULO
Solução:
Em um polinômio da forma: A.x^n + B.x^n-1 + C.x^n-2 + ..., a soma de suas raízes é dada pelo quociente -
B/A. No polinômio em questão, o coeficiente do termo x3 é nulo, logo, a soma de todas as suas raízes
é zero.
Resposta: letra b.
0
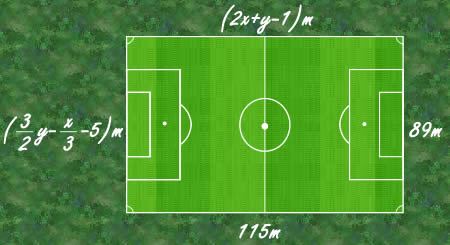
Na Figura está representado o retângulo de jogo de um campo de futebol. Determine...
By Smatias / Posted on 00:13 / Exercício, Função Quadrática
Na Figura está representado o retângulo de jogo de um campo de futebol. Determine  e
e  .
.
Resolução do exercício de matemática




Portanto, .
.
 e
e  .
.
Resolução do exercício de matemática




Portanto,
 .
.
0
 definida por
definida por  .
.
Determine:
Resolução do exercício de matemática:
1.



2.


3.


4.



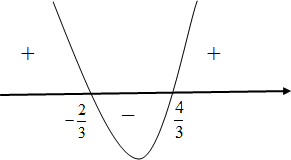
![S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[ S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[](http://www.atividadesdematematica.com/images/joomlatex/0f5d3a88f188b78ada22d18983083410.gif)
Exercício bem Legal de Função
By Smatias / Posted on 22:10 / Exercício, Função Quadrática
Função Quadrática
Exercício 1
Considere a função  definida por
definida por  .
.Determine:
1. os zeros da função.
2. o vértice e o eixo de simetria da parábola que representa graficamente a função.
3. dois objetos, distintos dos zeros, que tenham a mesma imagem.
4. os valores  de tais que
de tais que  .
.
 de tais que
de tais que  .
.Resolução do exercício de matemática:
1.



2.


Coordenadas do vértice: 

Eixo de simetria: 

3.
Os objetos pretendidos têm que estar à mesma distância do eixo de simetria.
Por exemplo:


Logo,  e
e  são dois objetos que têm a mesma imagem.
são dois objetos que têm a mesma imagem.
 e
e  são dois objetos que têm a mesma imagem.
são dois objetos que têm a mesma imagem.
Cálculo auxiliar:



![S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[ S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[](http://www.atividadesdematematica.com/images/joomlatex/0f5d3a88f188b78ada22d18983083410.gif)
0
12.345.679 x 27 = 333.333.333
Assim sucessivamente
12.345.679 x 63 = 777.777.777
Para obter o número 999.999.999 qual deve ser o produto?
Resposta
Qual o próximo numero?
By Smatias / Posted on 16:55 / Curiosidade, Exercício
Multiplicando... 12.345.679
12.345.679 x 18 = 222.222.22212.345.679 x 27 = 333.333.333
Assim sucessivamente
12.345.679 x 63 = 777.777.777
Para obter o número 999.999.999 qual deve ser o produto?
Resposta
0
Em uma caixa há duas bolas azuis, 3 bolas...
Em uma caixa há
duas bolas azuis, 3 bolas amarelas e 4 bolas pretas. Serão retiradas N bolas
dessa caixa, simultaneamente e de forma totalmente aleatória. O menor valor positivo
de N , para que se possa garantir que haverá bolas de todas as cores, é :
(A)
4 (B) 5 (C) 6 (D) 7 (E) 8
Comentário:
O menor valor
positivo de N , para que se possa garantir que haverá bolas de todas as cores
temos que supor que são retiradas 4 pretas + 3 amarelas + 1 azul, logo deverão
ser 08(oito) bolas.
0
Leonardo, Caio e Márcio são considerados suspeitos de praticar um crime. Ao serem interrogados por um delegado, Márcio disse que era ...
Leonardo, Caio e Márcio são considerados suspeitos de
praticar um crime. Ao serem interrogados por um delegado, Márcio disse que era
inocente e que Leonardo e Caio não falavam a verdade. Leonardo disse que Caio
não falava a verdade, e Caio disse que Márcio não falava a verdade.
A partir das informações
dessa situação hipotética, é correto afirmar que
A) os três rapazes mentem.
B) dois rapazes falam a
verdade.
C) nenhuma afirmação feita
por Márcio é verdadeira.
D) Márcio mente, e Caio
fala a verdade.
E) Márcio é inocente e
fala a verdade.
Comentário:
Nesta questão uma saída é a aplicação do
método da experimentação,supondo que Leo
fale a verdade não dará certo, mas ao supor que ele fale a mentira temos :
Márcio mente, Leo mente e Caio fala a verdade.
Assinar:
Comentários (Atom)

















