Números
Reais
O
principal motivo para que a maioria dos cursos de Cálculo comecem por um breve
estudo dos números reais é o fato de no Cálculo e na Análise, estuda-se o
comportamento de funções e o comportamento de uma função depende dos três
elementos importantes que a compõem: números Reais, números Racionais e números
irracionais.
Para entendermos os números Reais, deveremos primeiro estudar os
números, racionais e os números irracionais, uma vez que o mesmo é composto por
estes dois conjuntos numéricos.
Os números reais são números usados
para representar uma quantidade contínua (incluindo o zero e os negativos).
Números Naturais (N)
O conjunto de números naturais é representado pela letra N e é compostos por
números inteiros e positivos, além do zero. É indicado por:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...}
O símbolo N* é usado para indicar o conjunto de números naturais, sem o zero:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
12, ...}
Números Inteiros (Z)
O conjunto dos números inteiros, representado pela letra Z, é o conjunto dos
números naturais acrescido dos seus opostos negativos. Pode-se dizer que os
números inteiros expressam quantidades (inteiros positivos) e a
"falta" de quantidades (inteiros negativos).
O Conjunto dos Números Inteiros é
indicado por Z:
Z = {..., -5, -4, -3, -2, -1, 0 , 1, 2, 3, 4, 5, ...}
O símbolo Z* é usado para indicar o conjunto de números inteiros, sem o zero,
ou seja:
Z* = {..., -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, ...}
Como todos os números naturais também são números inteiros, dizemos que N é um
subconjunto de Z ou que N está contido em Z:
Alguns números inteiros apresentam uma série de características que os
diferenciam de outros inteiros e que torna possível agrupá-los em subconjuntos. Veja
alguns exemplos:
Números Primos
São chamados de primos os inteiros
diferentes 1 que só são divisíveis por 1 e por ele mesmo
ex: 2, 3, 5, 7, 11,13, 17, 19, etc.
Números Racionais (Q)
Quando dividimos um número inteiro (a) por outro número inteiro (b) obtemos um
número racional. Todo número racional sempre é representado por uma parte inteira
e por uma parte fracionária, a / b, Por exemplo:
Se a=6 e b=2,
obtemos o número racional 3,0.
Se a=1 e b=2,
obtemos o número racional 0,5. Ambos têm um número finito de casas após a
vírgula e são chamados de racionais de decimal exata.
Existem casos em que o número de casas após a vírgula é infinito. Por exemplo,
a=1 e b=8 nos dá o número racional 0,666666... É a chamada dízima periódica.
Podemos considerar que os números racionais englobam todos os números inteiros
e os que ficam situados nos intervalos entre os números inteiros.
Q = {a/b | a Z e b Z*}, ou seja, o
denominador deve sempre ser diferente de zero.
O símbolo Q* é usado para indicar o conjunto dos números racionais sem o zero:
Q* = Q - {0}
Como todos os números inteiros também são números racionais, dizemos que Z é um
subconjunto de Q ou que Z está contido em Q:
Números Irracionais (I)
Quando a divisão de dois números tem como resultado um número com infinitas
casas depois da vírgula que não se repetem periodicamente, obtemos um número
chamado de irracional. Não é possível situar um número irracional como um ponto
numa reta.
O número irracional mais famoso é o pi (p), inicial da palavra grega que
significa periferia, circunferência. Nos dias de hoje, já são conhecidos mais
de 1 bilhão de casas após a vírgula para este número graças aos computadores e
matemáticos de nossa época (p
= 3.1415926535897932384626433832795...)
Números Reais (R)
Como já foi dito anteriormente, o conjunto formado por todos os números
racionais e irracionais é o conjunto dos números reais, indicado por R.
Como todo número natural é inteiro, como todo número inteiro é racional e como
todo número racional é real, temos:
Indicamos por R* o conjunto de números reais sem o zero, ou seja,
R* = R - {0}
 , definida por
, definida por  .
. .
. .
. quanto a:
quanto a: , temos que
, temos que  .
.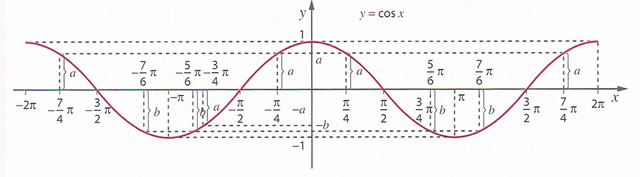
 é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo  , o que significa que a função cosseno assume os mesmos valores de
, o que significa que a função cosseno assume os mesmos valores de  em
em  , isto é
, isto é 
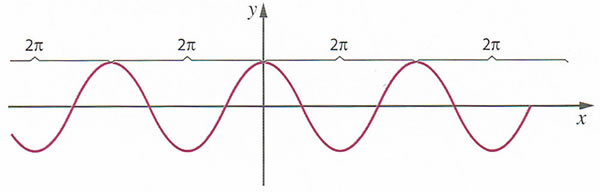
 admite zeros em
admite zeros em 
 são:
são:

 é uma função par, pois
é uma função par, pois  . Graficamente esta propriedade traduz-se pela existência de simetria relativamente ao eixo das ordenadas.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente ao eixo das ordenadas. não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 

![= \left[ { - 1,1} \right] = \left[ { - 1,1} \right]](http://www.atividadesdematematica.com/images/joomlatex/c421c8837a12e0801c59c41a50ee6545.gif)
 , definida por
, definida por  .
. .
. .
. quanto a:
quanto a: , sendo que a tangente,
, sendo que a tangente,  , não está definida sempre que o cosseno se anula, logo
, não está definida sempre que o cosseno se anula, logo  .
.
 é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo  , o que significa que a função tangente assume os mesmos valores de
, o que significa que a função tangente assume os mesmos valores de  em
em  , isto é
, isto é 

 admite zeros em
admite zeros em 
 não tem extremos.
não tem extremos. é uma função ímpar, pois
é uma função ímpar, pois  . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial. não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 


