0

Questão de concurso

By Smatias / Posted on 12:40 /
CONCURSO SECRETARIA MUNICIPAL DE SAÚDE/2005 – CESGRANRIO) – (questão de sistemas de medidas)

Raquel saiu de casa às 13h 45min, caminhando até o curso de inglês que fica a 15 minutos de sua casa, e chegou na hora da aula cuja duração é de uma hora e meia. A que horas terminará a aula de inglês?

a) 14h

b) 14h 30min

c) 15h 15min

d) 15h 30min

e) 15h 45min



Solução:

Basta somarmos todos os valores mencionados no enunciado do teste, ou seja:

13h 45min + 15 min + 1h 30 min = 15h 30min

Gabarito: D
Read More
0

Com os algarismos x, y e z formam-se os números de dois algarismos xy e yx, cuja soma é

By Smatias / Posted on 22:56 /

Desafio do X,Y,Z



Com os algarismos x, y e z formam-se os números de dois algarismos xy e yx, cuja soma é o número de três algarismos zxz. Quanto valem x, y e z?

Esta é bem inteligente..
CONFIRA O CANAL MATCÁLCULO
Resposta AQUI
Read More
0

Problema com Idades

By Smatias / Posted on 02:10 /

Problema com Idade sempre é legal

A idade atual de Jachkero àgua é a diferença entre 5/8 da idade que ele terá daqui a 18 anos e os 2/3 da idade que ele teve há 5 anos. A idade  de Jachkero àgua é:

 (A) 14 (B) 13 (C) 10 (D) 8 anos e 4 meses (E) 7 anos e 6 meses

essa deu um pouco de trabalho...
É interresante tentar antes de ver a resposta...


Mas a resposta é jachkero-agua-sua-idade-e.html 


Read More
1

Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se

By Smatias / Posted on 18:13 /

E agora

 Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se, repartindo antes o vinho igualmente.
Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?

Resposta
Read More
0

A soma de todas as raízes da equação

By Smatias / Posted on 00:33 /
A soma de todas as raízes da equação x^4 - 25x^2 + 144 = é igual a
a) 16 b) 0 c) 9 d) 49 e) 25


CONFIRA O CANAL MATCÁLCULO

Solução:
Em um polinômio da forma: A.x^n + B.x^n-1 + C.x^n-2 + ..., a soma de suas raízes é dada pelo quociente -
B/A. No polinômio em questão, o coeficiente do termo x3 é nulo, logo, a soma de todas as suas raízes
é zero.
Resposta: letra b.
Read More
0

Na Figura está representado o retângulo de jogo de um campo de futebol. Determine...

By Smatias / Posted on 00:13 / ,
Na Figura está representado o retângulo de jogo de um campo de futebol. Determine x e y.
campo de futebol
Resolução do exercício de matemática

 \left\{ {\begin{array}{*{20}{c}} {2x + y - 1 = 115} \\ {\frac{3}{2}y - \frac{x}{3} - 5 = 89} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2x + 116} \\ {\frac{3}{2}\left( { - 2x + 116} \right) - \frac{x}{3} = 94} \end{array}} \right. \Leftrightarrow

\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2x + 116} \\ { - 3x + 174 - \frac{x}{3} = 94} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2x + 116} \\ { - 3x - \frac{x}{3} = - 80} \end{array}} \right. \Leftrightarrow

\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2x + 116} \\ { - 9x - x = - 240} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2x + 116} \\ { - 10x = - 240} \end{array}} \right. \Leftrightarrow

\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = - 2 \times 24 + 116} \\ {x = 24} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = 68} \\ {x = 24} \end{array}} \right.

Portanto, x = 24{\text{ e }}y = 68.
Read More
0

Exercício bem Legal de Função

By Smatias / Posted on 22:10 / ,

Função Quadrática

Exercício 1
Considere a função h definida por h\left( x \right) = 2{x^2} - \frac{4}{3}x.
Determine:
1. os zeros da função.
2. o vértice e o eixo de simetria da parábola que representa graficamente a função.
3. dois objetos, distintos dos zeros, que tenham a mesma imagem.
4. os valores x de tais que h\left( x \right) > \frac{{16}}{9} .

Resolução do exercício de matemática:

1.

h\left( x \right) = 0 \Leftrightarrow 2{x^2} - \frac{4}{3}x = 0 \Leftrightarrow x\left( {2x - \frac{4}{3}} \right) = 0 \Leftrightarrow x = 0 \vee 2x - \frac{4}{3} = 0 \Leftrightarrow

\Leftrightarrow x = 0 \vee 2x = \frac{4}{3} \Leftrightarrow x = 0 \vee x = \frac{2}{3}

S = \left\{ {0,\frac{2}{3}} \right\}

2.

h\left( x \right) = 2{x^2} - \frac{4}{3}x = 2\left( {{x^2} - \frac{2}{3}x} \right) = 2\left( {{x^2} - \frac{2}{3}x + {{\left( {\frac{1}{3}} \right)}^2} - {{\left( {\frac{1}{3}} \right)}^2}} \right) =

= 2\left( {{x^2} - \frac{2}{3}x + {{\left( {\frac{1}{3}} \right)}^2}} \right) - {\left( {\frac{1}{3}} \right)^2} \times 2 = 2{\left( {x - \frac{1}{3}} \right)^2} - \frac{2}{9}

Coordenadas do vértice:   V\left( {\frac{1}{3}, - \frac{2}{9}} \right)

Eixo de simetria:   x = \frac{1}{3}

3.

Os objetos pretendidos têm que estar à mesma distância do eixo de simetria.
Por exemplo:

\frac{1}{3} - 2 = - \frac{5}{3}

\frac{1}{3} + 2 = \frac{7}{3}

Logo, - \frac{5}{3} e \frac{7}{3}  são dois objetos que têm a mesma imagem.

4.

h\left( x \right) > \frac{{16}}{9} \Leftrightarrow 2{x^2} - \frac{4}{3}x > \frac{{16}}{9} \Leftrightarrow 2{x^2} - \frac{4}{3}x - \frac{{16}}{9} > 0

Cálculo auxiliar:

2{x^2} - \frac{4}{3}x - \frac{{16}}{9} = 0 \Leftrightarrow x = \frac{{\frac{4}{3} \pm \sqrt {{{\left( { - \frac{4}{3}} \right)}^2} - 4 \times 2 \times \left( { - \frac{{16}}{9}} \right)} }}{{2 \times 2}} \Leftrightarrow

\Leftrightarrow x = \frac{{\frac{4}{3} \pm 4}}{4} \Leftrightarrow x = \frac{{\frac{{16}}{3}}}{4} \vee x = \frac{{ - \frac{8}{3}}}{4} \Leftrightarrow x = \frac{4}{3} \vee x = - \frac{2}{3}

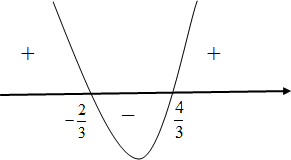
Funções

S = \left] { - \infty , - \frac{2}{3}} \right[ \cup \left] {\frac{4}{3}, + \infty } \right[
Read More
0

Qual o próximo numero?

By Smatias / Posted on 16:55 / ,

Multiplicando... 12.345.679

12.345.679 x 18 = 222.222.222
12.345.679 x 27 = 333.333.333

 Assim sucessivamente

12.345.679 x 63 = 777.777.777

Para obter o número 999.999.999 qual deve ser o produto?

Resposta


Read More
0

Em uma caixa há duas bolas azuis, 3 bolas...

By Smatias / Posted on 20:34 / ,
Em uma caixa há duas bolas azuis, 3 bolas amarelas e 4 bolas pretas. Serão retiradas N bolas dessa caixa, simultaneamente e de forma totalmente aleatória. O menor valor positivo de N , para que se possa garantir que haverá bolas de todas as cores, é :
(A) 4           (B) 5        (C) 6           (D) 7       (E) 8



Comentário:
O menor valor positivo de N , para que se possa garantir que haverá bolas de todas as cores temos que supor que são retiradas 4 pretas + 3 amarelas + 1 azul, logo deverão ser 08(oito) bolas.
Read More
0

Leonardo, Caio e Márcio são considerados suspeitos de praticar um crime. Ao serem interrogados por um delegado, Márcio disse que era ...

By Smatias / Posted on 20:32 / ,
Leonardo, Caio e Márcio são considerados suspeitos de praticar um crime. Ao serem interrogados por um delegado, Márcio disse que era inocente e que Leonardo e Caio não falavam a verdade. Leonardo disse que Caio não falava a verdade, e Caio disse que Márcio não falava a verdade.
A partir das informações dessa situação hipotética, é correto afirmar que
A) os três rapazes mentem.
B) dois rapazes falam a verdade.
C) nenhuma afirmação feita por Márcio é verdadeira.
D) Márcio mente, e Caio fala a verdade.
E) Márcio é inocente e fala a verdade.

Comentário:

Nesta questão uma saída é a aplicação do método da experimentação,supondo que  Leo fale a verdade não dará certo, mas ao supor que ele fale a mentira temos : Márcio mente, Leo mente e Caio fala a verdade.
Read More
Assinar: Postagens (Atom)